A lamina occupies the region inside the circle x 2 y 2 = 2 y but outside the circle x 2 y 2 = 1 Find the center of mass if the density at any point is inversely proportional to its distance from the origin close Start your trial now!The given polar equation was a circle of radius 1/2centered at (1/2,0) since r =cosθ =⇒ r2 =rcosθ Converting to rectangular coordinates we obtain x2y2 =x =⇒ (x−1/2)2y2 =1/4 However, we were unsure which values of θ were necessary to generate a complete circle ItArrow_forward Buy Find launch

Ex 8 2 2 Find Area Bounded By X 1 2 Y2 1 And X2 Y2 1
Green's theorem circle x^2+y^2=1
Green's theorem circle x^2+y^2=1-Consider the triangle T ⊂ S with vertices (0,0), (1/2,1/2), (1/2,1) Thus, T is defined by the inequalities 0 < x < y < 2x < 1 For every (x,y) in T, xy > x2 and x2 y2 < 5x2 Show that all solutions of y'= \frac {xy1} {x^21} are of the form y=xC\sqrt {1x^2} without solving the ODE Show that all solutions of y′ = x21xy1Suppose mathf(x,y) = x^2 y^2/math Let's look at the partial derivatives of this function math\displaystyle\frac{\partial f}{\partial x}= 2x/math math




With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used To Determine Whether Or Not A Point Lies On The Unit Circle Study Com
Let C be the positively oriented circle X^2Y^2=1 Use greens theorem to evaluate the line integral \(\int_{c}^{}19ydx17xdy\) The circle with equation x^2 y^2 = 1 intersects the line y= 7x5 at two distinct points A and B Let C be the point at which the positive xaxis intersects the circle The angle ACB is Updated On This browser does not support the video element 38 kIps the circle insideout That is, points outside the circle get mapped to points inside the circle, and points inside the circle get mapped outside the circle De nition 01 Let Cbe a circle with radius rand center O Let Tbe the map that takes a point Pto a point P0on the ray OPsuch that OPOP0= r2 Then, Tis an inversion in the circle C 2
Circle and spherefind the equation of the chord of contact of (1,1) wrto the circle x^2y^2=1Problem 33 Medium Difficulty Find a parametrization for the circle $(x2)^{2}y^{2}=1$ starting at $(1,0)$ and moving clockwise once around the circle, using them central angle $\theta$ in the accompanying figure as the parameterWe note that the integrand 1x^2y^2 can be written 1 (x^2 y^2) Hence, we identify the pattern and change to polar coordinates In polar coordinates, x = r \cos \theta and y = r \sin \theta Thus, x^2 y^2 = r^2 In polar coordinates, the differential area element dx dy = r dr d\theta We can now write the integrand as 1x^2 y^2 = 1 (x
Both x and y are functions of t so you can differentiate the expression x2 y2 = 1 to get 2x dx/dt 2y dy/dt = 0 Substitute dx/dt = y to get 2y(x dy/dt) = 0 Hence if y is not zero then dy/dt = x Now draw a circle with center at the origin and mark some point PThe blue colored unit circle if your set $x^2y^2 = 1$ The remaining white space is the complement of the unit circle You want to show that this complement is openIf we rewrite this as x 3 2 y 3 2 = 1, then we can write x 3 = cost, y 3 = sint 1




Circles
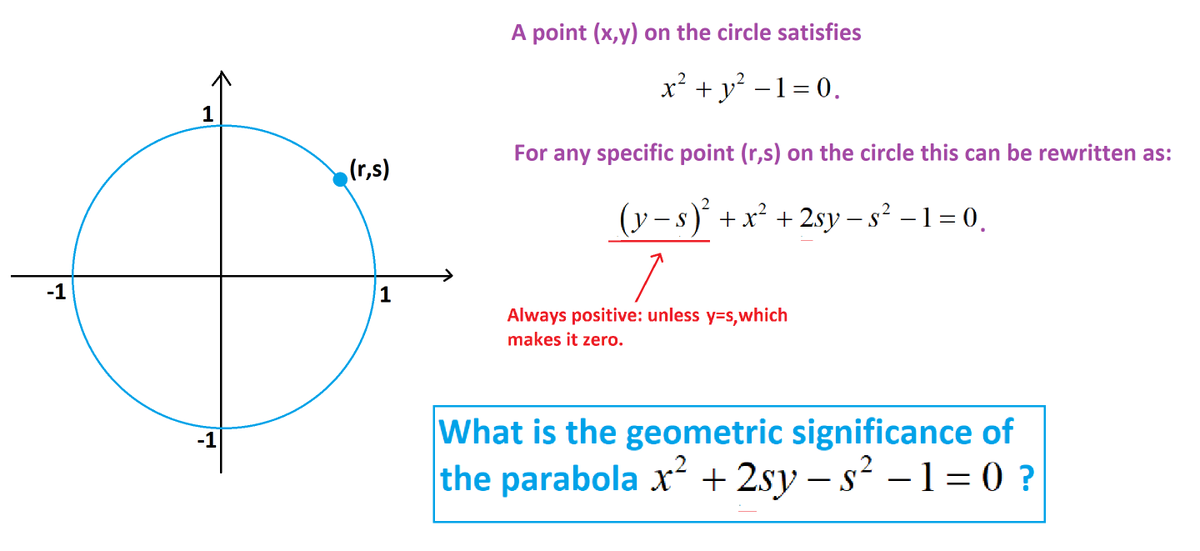



James Tanton The Equation Of The Unit Circle X 2 Y 2 1 Can Be Rewritten Y S 2 X 2 2sy S 2 1 0 With A Term That Is Always Non Negative And A Quadratic Term
X^2y^2=1 radius\x^26x8yy^2=0 center\ (x2)^2 (y3)^2=16 area\x^2 (y3)^2=16 circumference\ (x4)^2 (y2)^2=25 circlefunctioncalculator x^2y^2=1 enQuestion 1961 Find the radius and center of each circle 12 (x 2)^2 (y 3)^2 = 16 13 x^2 (y 4)^2 = 8 14 (x 1)^2 (y 2)^2 = 12 15 (x 6)^2(1)To come up with this, remember that we can parameterize a circle x2 y2 = 1 in R2 by = cos t, = sin (and, as increases, this goes around the circle counterclockwise) Here, we're looking at x 2y = 9;



If The Chord Y Mx 1 Of The Circle X 2 Y 2 1 Subtends An Angle Of Measures 45 Degree At The Major Segment Of The Circle Then Value Of M Is Sarthaks Econnect Largest




If 2x 2 2y 2 2x 2y 1 0 Then What Is The Value Of X Y Quora
Example a=1, b=2, r=3 (x−1)2 (y−2)2 = 32 Expand x2 − 2x 1 y2 − 4y 4 = 9 Gather like terms x2 y2 − 2x − 4y 1 4 − 9 = 0 And we end up with this x2 y2 − 2x − 4y − 4 = 0 It is a circle equation, but "in disguise"!Cylinder x2 y2 = 4, oriented clockwise when viewed from above Solution Let S be the part of the plane 3x 2y z = 6 that lies inside the cylinder x 2 y 2 = 1, oriented downwardAnswer to Let C be the positively oriented circle x^2 y^2 = 1 Use Green's theorem to evaluate the C integral 3ydx 15xdy By signing up,



Find The Area Of The Region Enclosed Between The Two Circles X 2 Y 2 1 And X 1 2 Y 2 1 Sarthaks Econnect Largest Online Education Community




Find The Equation Of The Normal To The Circle X 2 Y 2 5 At The
Circle x 2y =1 •Solution Solve equations ∇f= λ ∇g and g(x,y)=1 using Lagrange multipliers Constraint g(x, y)= x2y2=1 Using Lagrange multipliers, f x = λg x f y = λg y g(x,y) = 1 which become Continued • 2x= 2xλ (9)Fimplicit(fun) gives out the right hyperbolaformula Star Strider onIf the chord y = mx 1 of the circle x^2 y^2 = 1 subtends an angle 45^o at the major segment of the circle, then value of m is



Ellipses And Hyperbolae




Ex 8 2 2 Find Area Bounded By X 1 2 Y2 1 And X2 Y2 1
164E Exercises for Section 164 For the following exercises, evaluate the line integrals by applying Green's theorem 1 ∫C2xydx (x y)dy, where C is the path from (0, 0) to (1, 1) along the graph of y = x3 and from (1, 1) to (0, 0) along the graph of y = x oriented in the counterclockwise direction 2 ∫C2xydx (x y)dy, where CT 0, 2 We apply the same procedure to eliminate the parameter, namely square x and y, and add the terms x 2 y 2 = sin 2 (t) cos 2 (t) = 1 The locus of the centres of the circles, which touch the circle, x^2 y^2 = 1 externally, also touch the yaxis and lie in the first quadrant, is asked in Mathematics by Jagan (211k points) jee mains 19;




R 2 Circles




System Of Circles
the radius of the circle is √2 Join radii to the points where the line y=1 cuts the circle from the origin to the line along the yaxis is 1, the radius is √2, so the other side of the triangle must be 1 so you have a 45, 45 90 triangle, so is the other one Both of them make a 90º at the centre the area of those two triangles is 1/2X^{2}\left(2y\right)xy^{2}1=0 Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^{2 It is the equation of a circle Probably you can recognize it as the equation of a circle with radius r=1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k) is (xh)^2(yk)^2=r^2



A Circle Can Be Drawn With Any Center And Any Radius Geogebra
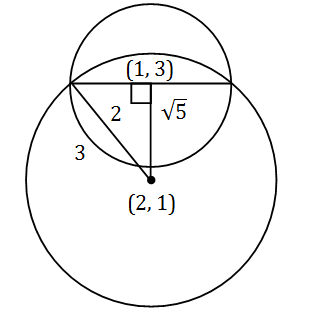



If One Of The Diameters Of The Circle X 2 Y 2 2x 6y 6 0 Is A Chord Of Another Circle C Whose Center Is At 2 1 Then Its Radius Is
Question Find the radius of a circle x^2 y^2 4x 4y 1 = 0 Answer by ewatrrr() (Show Source) You can put this solution on YOUR website!So when you see something like that think "hmm that might be a circle!"2 Find the area bounded by curves (x – 1)^2 y^2 = 1 and x^2 y^2 = 1 application of integration,applications of integration,application of integrals,i



Circle Has The Equation X 2 Y 2 2x 2y 14 0 How Do You Graph The Circle Using The Center H K Radius R Socratic
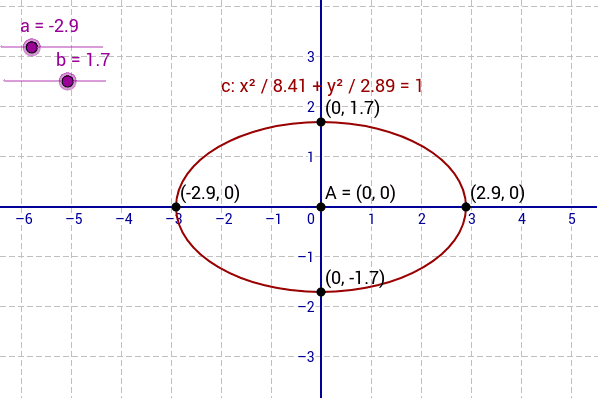



Equation Of An Ellipse X A 2 Y B 2 1 Geogebra
Let RS be the diameter of the circle x^2y^2=1, where S is the point (1,0) Let P be a variable apoint (other than R and S ) on the circle and tangents to the circle at S and P meet at the point QThe normal to the circle at P intersects a line drawn through Q parallel to RS at point E then the locus of E passes through the point(s) (A) (1/3,1/sqrt3) (B) (1/4,1/2) (1/3,1/sqrt3) (D) (1/4,1/2)The area of the region bounded by the circle x^2 y^2 = 1 is A 2π sq units # NCERT The area of the region bounded by the circle is A 2π sq units B π sq units C 3π sq units D 4π sq units Post Answer Answers (1) I infoexpert22 B) The circle The circle(a) Find the center and radius of the circle (b) Graph the circle Note To correctly identify the center of the circle we have to place the equation in the standard form The standard form is (x h) 2 (yk) 2 = r 2 (x (1)) 2 (y2) 2 = (3) 2 Now, you can identify the center correctly



Differential And Integral Calculus To The Circle X 4 2 Y 3 2 25 At The Point 7 1 7 Find The Equations Of The Tangents To The Hyperbola4x2 Gy2 36
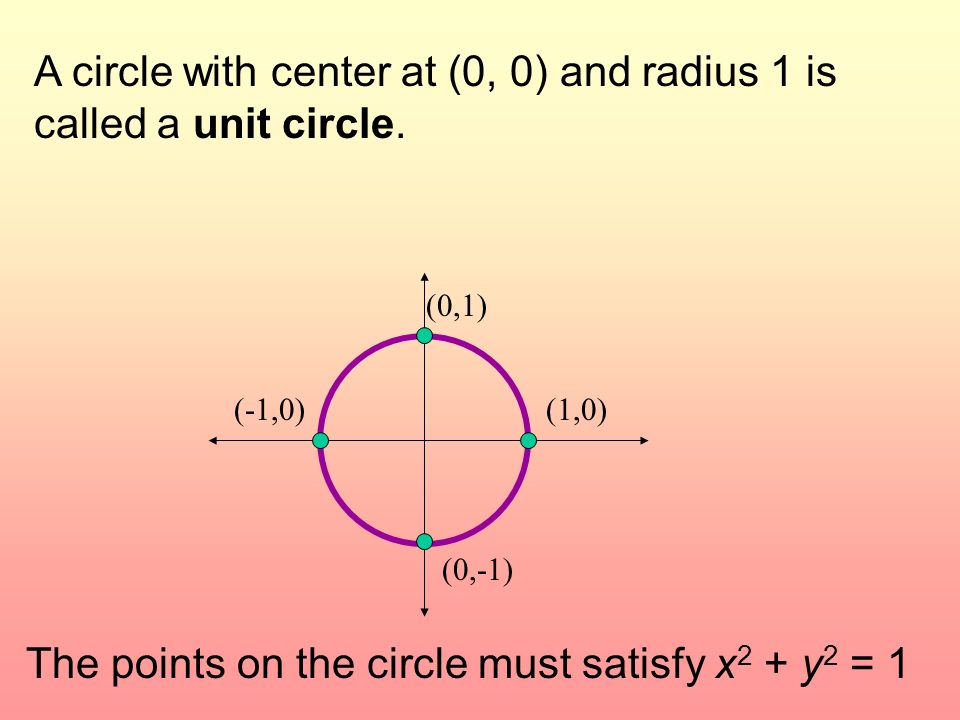



Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download
If the circle C 1 x 2 y 2 = 16 intersects another circle C 2 of radius 5 in such a manner that the common chord is of maximum length and has a slope equal to 3/4, then the coordinates of the centre of C 2 areGraph x^2y^2=1 x2 − y2 = −1 x 2 y 2 = 1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive − x 2 y 2 = 1 x 2 y 2 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of anThe other particle moves along the curve C 2, the bottom half of the circle defined by x 2 (y1) 2 = 1, as shown in Figure 1532 Force is measured in pounds and distances are measured in feet Find the work performed by moving each particle along its path




C Is The Circle With The Equation X 2 Y 2 1 Brainly Com




An Example Of A Hyperbola Of Equation X 2 A 2 Y 2 B 2 1 With Download Scientific Diagram
gives out a circle, whereas fun = @(x,y) x^2 y^2 1;Use a double integral to find the area of the region inside the circle (x 1)^2 y^2=1 and outside the circle x^2y^2=1 Get more help from Chegg Solve itX 2 y 2 = cos 2 (t) sin 2 (t) = 1 This is the equation of the unit circle and so the two parametric equations are a parameterization of the unit circle Now, consider x = sin(t), y = cos(t);




The Equation Of A Circle Of Radius 1 Touching The Circles X 2 Y




6 A Plot Of The Unit Circle Satisfying X 2 Y 2 1 Download Scientific Diagram
The equation of the unit circle is \(x^2y^2 = 1\) It is important because we will use this as a tool to model periodic phenomena We "wrap" the number line about the unit circle by drawing a number line that is tangent to the unit circle at the point \((1, 0)\) We wrap the positive part of the number line around the unit circle in thePythagoras Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides x 2 y 2 = 1 2 But 1 2 is just 1, so x 2 y 2 = 1 (the equation of the unit circle) Also, since x=cos and y=sin, we get (cos(θ)) 2 (sin(θ)) 2 = 1 a useful "identity" Important Angles 30°, 45° and 60° You should try to rememberFind the volume under the surface f (x, y) = 1 x 2 y 2 1 over the sector of the circle with radius a centered at the origin in the first quadrant, as shown in Figure 1434 Solution † † margin Figure 1434 The surface and region R used in Example 1433




If One Of The Diameters Of The Circle X 2 Y 2 2x 6y 6 0 Is A Chord To The Circle With Centre 2 1 Then Radius Of The Circle Is Ans 3



Find The Area Inside The Circle X 2 Y 2 36 Above Chegg Com
0 votes 1 answerX^2y^2=1 radius\x^26x8yy^2=0 center\(x2)^2(y3)^2=16 area\x^2(y3)^2=16 circumference\(x4)^2(y2)^2=25 circleequationcalculator x^2y^2=1 enSo, the distance between the circle and the point will be the difference of the distance of the point from the origin and the radius of the circle Using the Distance Formula , the shortest distance between the point and the circle is ( x 1) 2 ( y 1) 2 − r Note that the formula works whether P is inside or outside the circle



1



Solved The Figure Shows A Fixed Circle C1 With Equation X 1 2 Y 2 1 And A Shrinking Circle C2 With
First week only $499!Answer to Evaluate \int_C (2 x^2y)ds where C is the upper half of the unit circle x^2 y^2 = 1 By signing up, you'll get thousands ofHi Standard Form of an Equation of a Circle is where Pt(h,k) is the center and r is the radius x^2 y^2 4x 4y



Question De065 Socratic
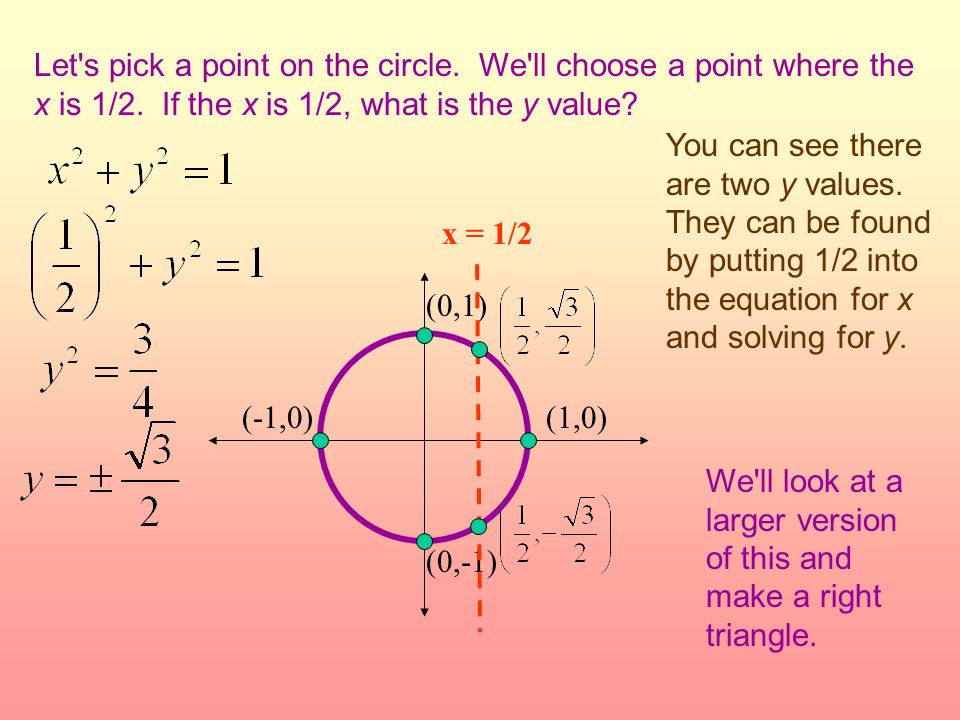



Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download
In mathematics, the rational points on the unit circle are those points (x, y) such that both x and y are rational numbers ("fractions") and satisfy x 2 y 2 = 1 The set of such points turns out to be closely related to primitive Pythagorean triplesConsider a primitive right triangle, that is, with integer side lengths a, b, c, with c the hypotenuse, such that the sides have no commonThe question can be solved easily once, we draw the graph of x 2 y 2 = 1 and ∣ y ∣ = x 1 The two curves when plotted on a graph sheet should be look like has been shown above Here, we are to find the area of the shaded regionThe given equation is for a unit circle The given points do not lie on the circle So, we cannot have a tangent line to the circle at either of those points It is possible, however, to draw a line that is tangent to the circle that passes throug



1



Exercises Involving Distance And Circles
Algebra Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yoffset from origin



How Do You Graph X 2 Y 2 1 Socratic
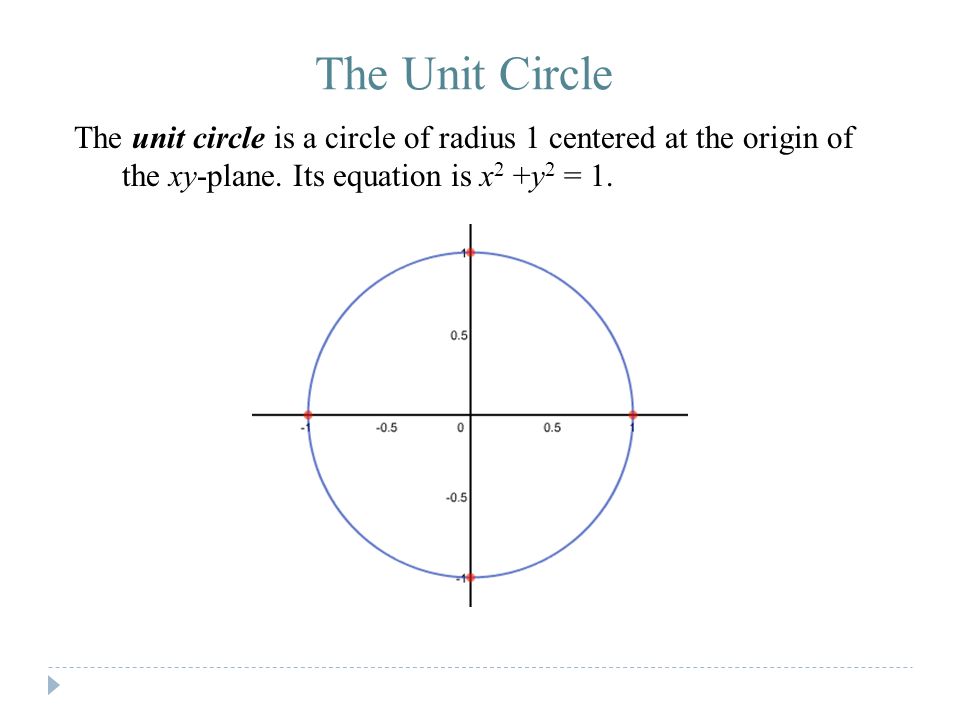



The Unit Circle The Unit Circle Is A Circle Of Radius 1 Centered At The Origin Of The Xy Plane Its Equation Is X 2 Y 2 Ppt Download




With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used To Determine Whether Or Not A Point Lies On The Unit Circle Study Com
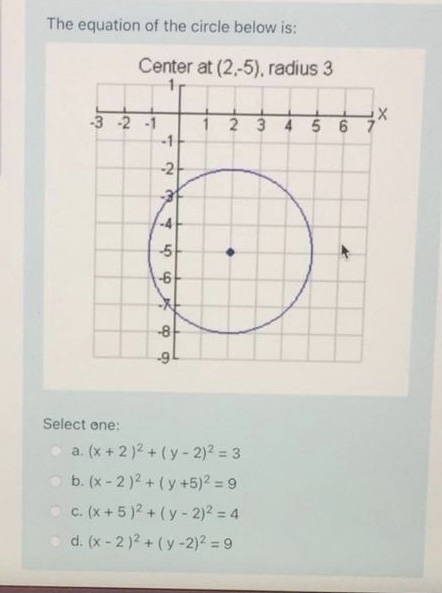



Answered The Equation Of The Circle Below Is Bartleby




How Do You Graph X 2 Y 2 4 Socratic
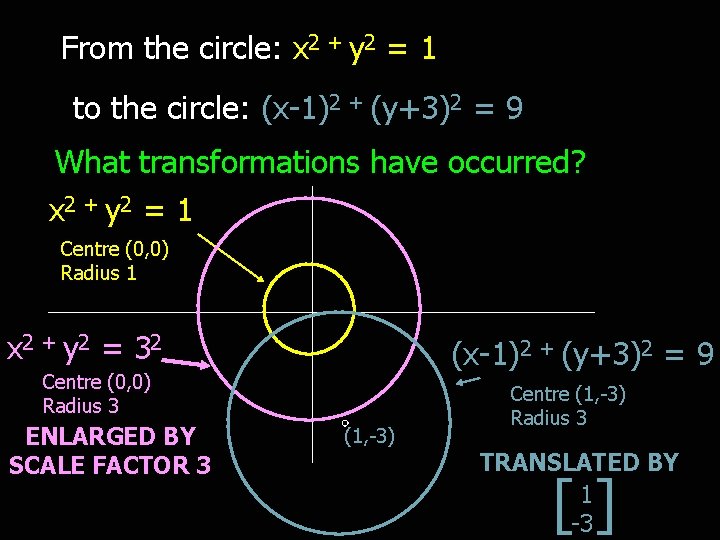



Circles Revision Transformations Intercepts Using The Discriminant Chords
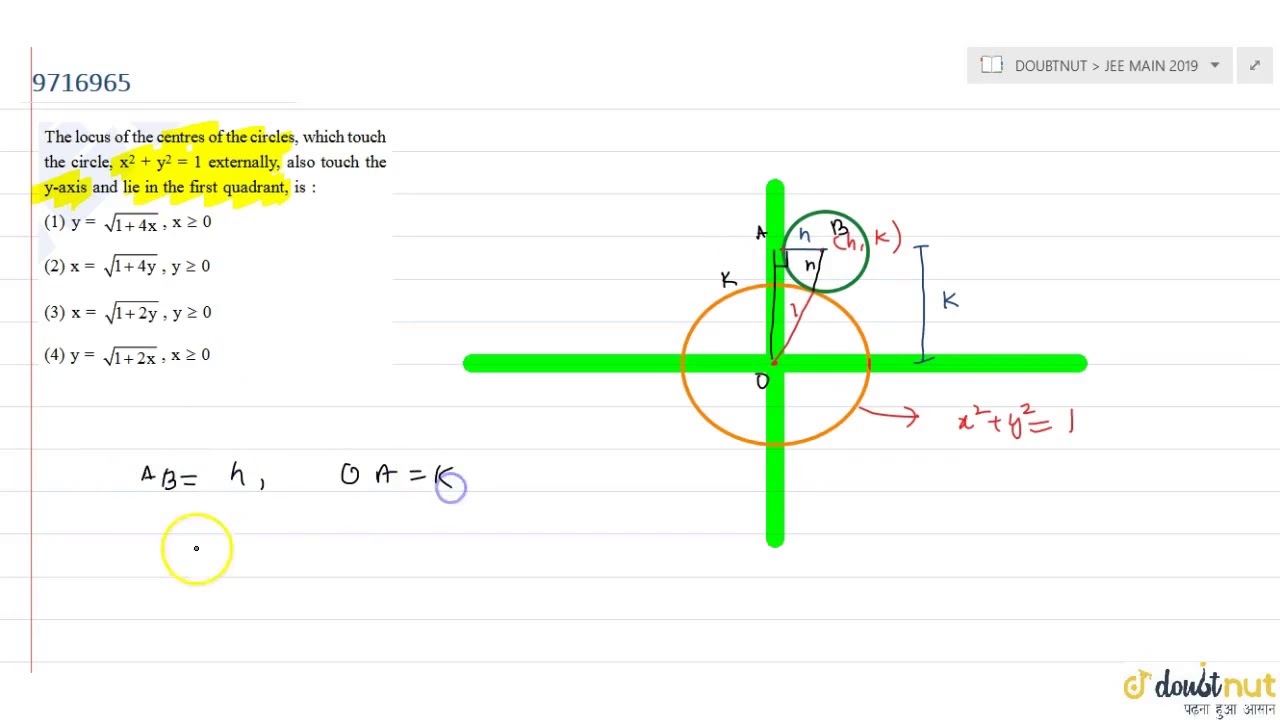



The Locus Of The Centres Of The Circles Which Touch The Circle X 2 Y 2 1 Externally Also Touch Youtube
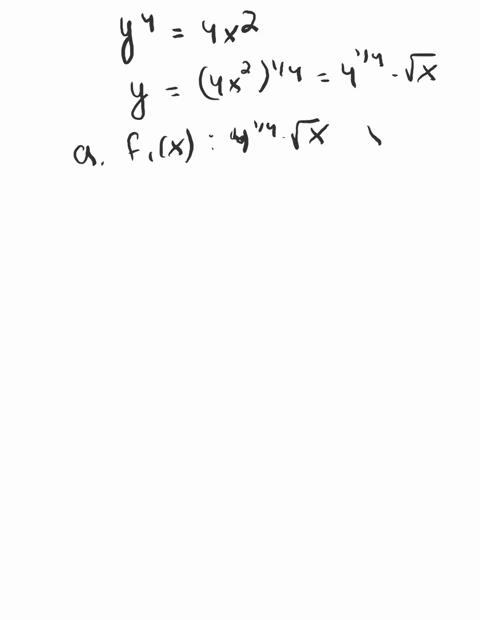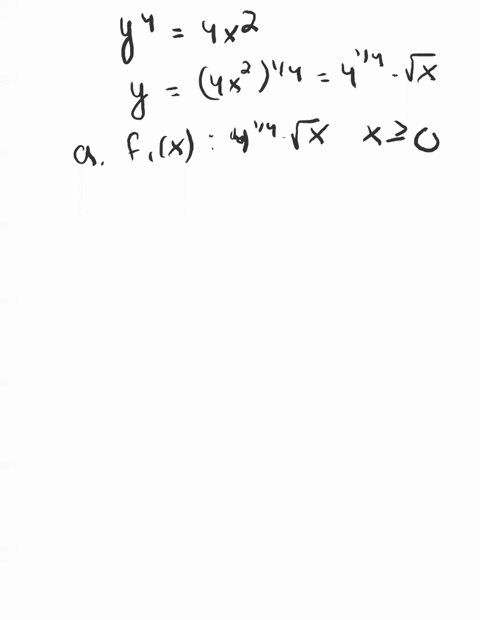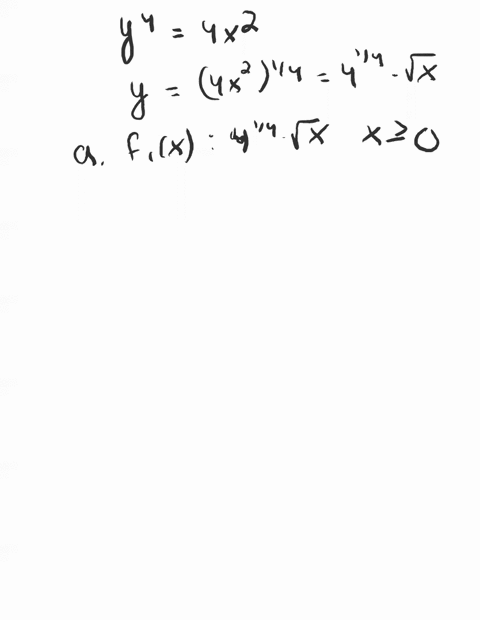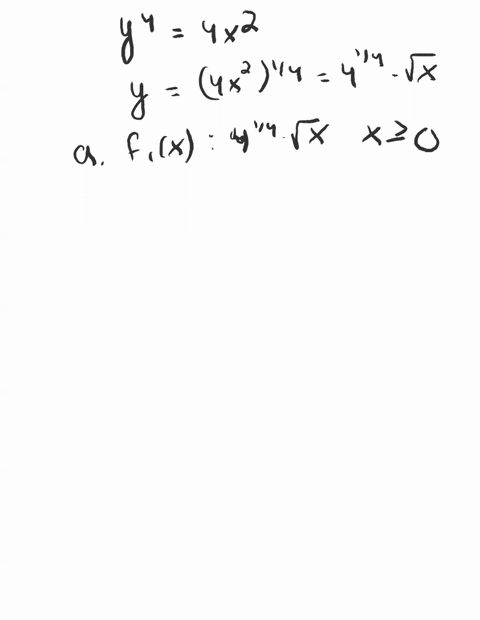



Solved The Unit Circle X 2 Y 2 1 Consists Of




The Equation Of The Diameter Of The Circle X 2 Y 1 16 Which Bisects The Chord Cut Off Brainly In



Conics Circles Ellipse



The Area Of The Region Bounded By The Circle X2 Y2 1 Is Studyrankersonline



Physical Applications Of Line Integrals Page 2
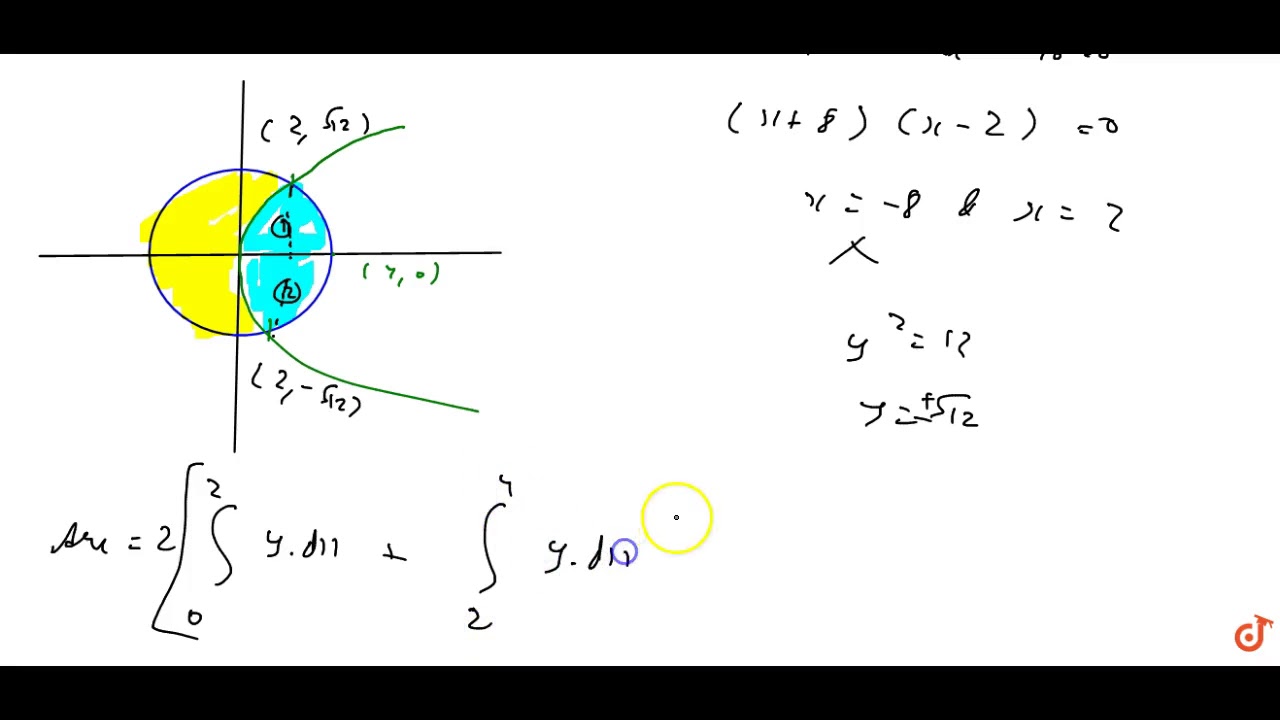



The Area Of The Circle X 2 Y 2 16 Exterior To The Parabola Y 2 6x Is A 4 3 4pi Sqrt 3 Youtube




14 1 Functions Of Several Variables Mathematics Libretexts




Example 1 Find Area Enclosed By Circle X2 Y2 Examples




A Tangent To The Circle X 2 Y 2 1 Through The Point 0 5



How Do You Determine The Domain And Range Of The Relation X 2 Y 2 1 And X 2 Y 2 100 I Know It Makes A Circle But I M Just Confused About The Enotes Com



Www Brewtoncityschools Org Cms Lib Al Centricity Domain 133 10 8 Equations Of Circle Pdf



Solution Find The Center And Radius Of The Circle X 2 Y 2 49 I 39 M Not Sure But I Have Used The Formula X H 2 Y K 2 Sq Root Of 49 And
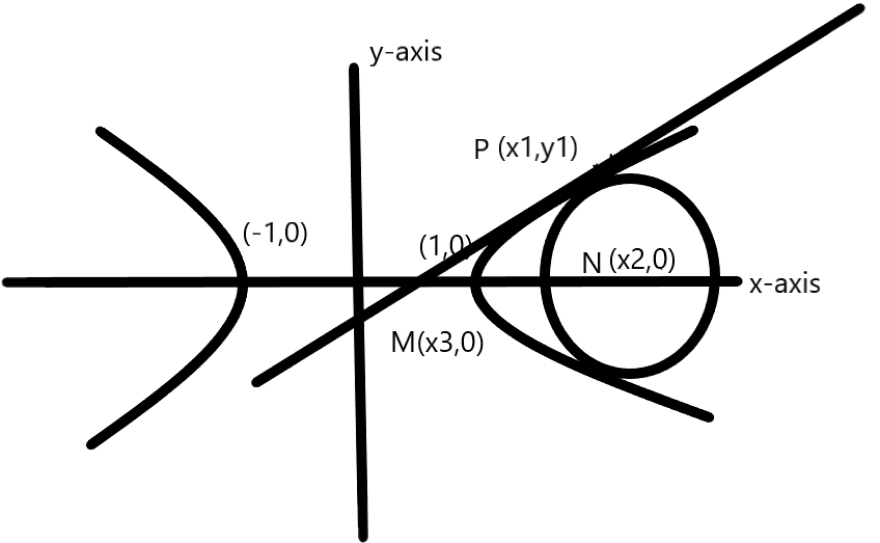



Consider The Hyperbola Hx2 Y2 1 And Circle S With The Class 11 Maths Cbse



Circle



Http Www Standrewspaisley Com Uploads 6 0 2 3 Circle Pupil Booklet Pdf




The Normalized Vector Field 16 For A Circle Path Described By F X Y Download Scientific Diagram




R 2 Circles




System Of Circles




Using Integration Find The Area Of The Region X Y X2 Y2 1 X Y Mathematics Shaalaa Com




Solution Find The Value Of K For Which The Equation X 2 Y



The Centres Of The Circles X 2 Y 2 1 X 2 Y 2 6x 2y 1 Sarthaks Econnect Largest Online Education Community
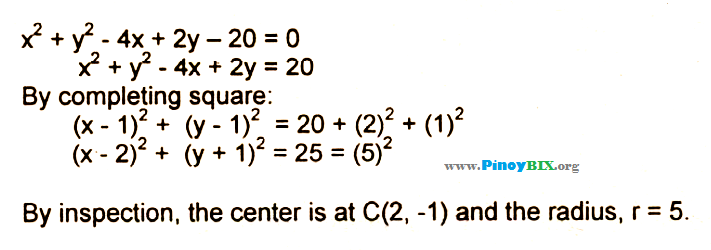



Solution The Equation X 2 Y 2 4x 2y 0 Describes




The Lines Y 1 2 X And Y 1 2 X Are Tangents To A Gauthmath



Http Www Nicolet K12 Wi Us Faculty Dgibbon Circle ellipse answer sheet pdf Pdf




2 1 Plot Of Circle X 2 Y 2 1 And The Definitions Of Cos 8 And Sin Download Scientific Diagram
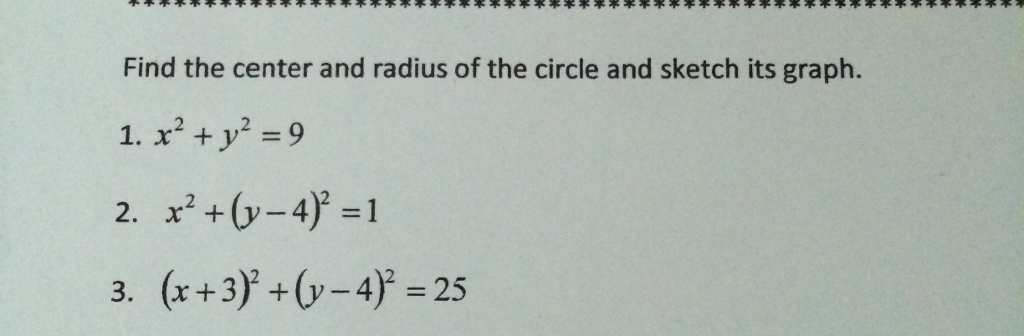



Find The Center And Radius Of The Circle And Sketch Chegg Com



Math Help



1




Ex 8 2 6 Smaller Area Enclosed By Circle X2 Y2 4 Line
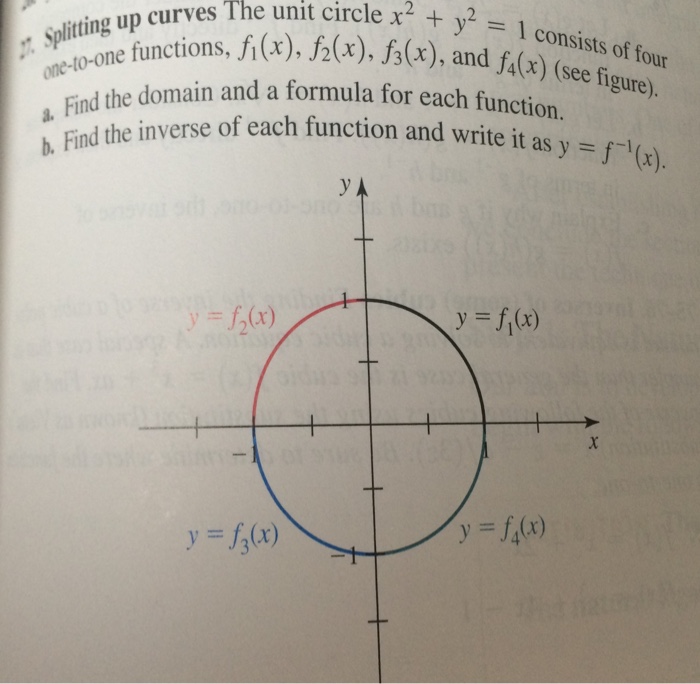



Splitting Up Curves The Unit Circle X 2 Y 2 1 Chegg Com
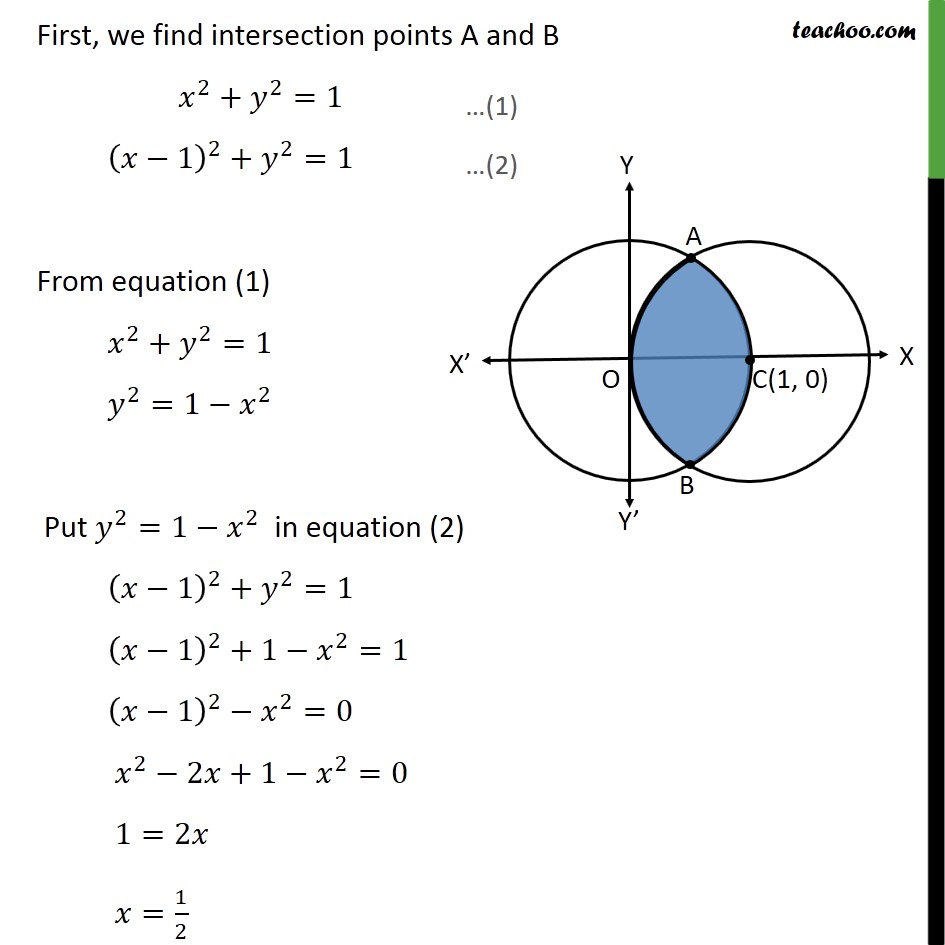



Ex 8 2 2 Find Area Bounded By X 1 2 Y2 1 And X2 Y2 1
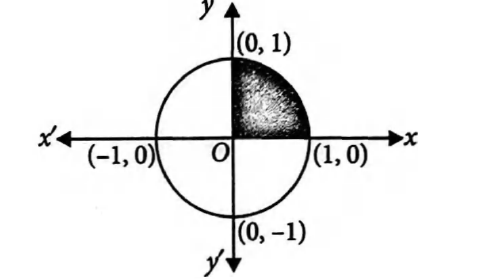



The Area Bounded By The Curve X2 Y2 1 In First Quadrant Is



What Is The Graph Of X 2 Y 2 Z 2 1 Quora



Www Toppr Com Ask Question The Point Of The Circle X 12 Y 12 1 Which




Using Integration Find Area Of Region X Y X 2 Y 2 1 X Y
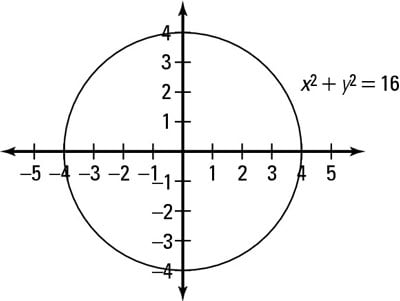



2 Ways To Graph A Circle Dummies




Sketch The Circles Y 2 X 2 1 And Y 2 X 3 2 4 There Is A Line With A Positive Slope That Is Tangent To Both Circles Determine The




For The Circle X 2 Y 2 2x 6y 1 0 The Chord Of Minimum Len




Is X 2 Y 2 1 Merely Frac 1x Rotated 45 Circ Mathematics Stack Exchange
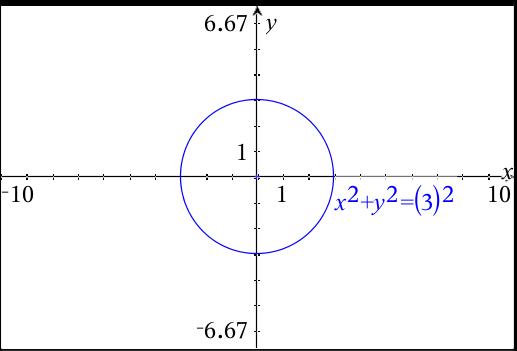



How Do You Graph X 2 Y 2 9 And What Are Its Lines Of Symmetry Socratic




Complex Numbers Absolute Value




A Circle X 2 Y 2 1 Cuts The Line X Y K And Makes Chord With
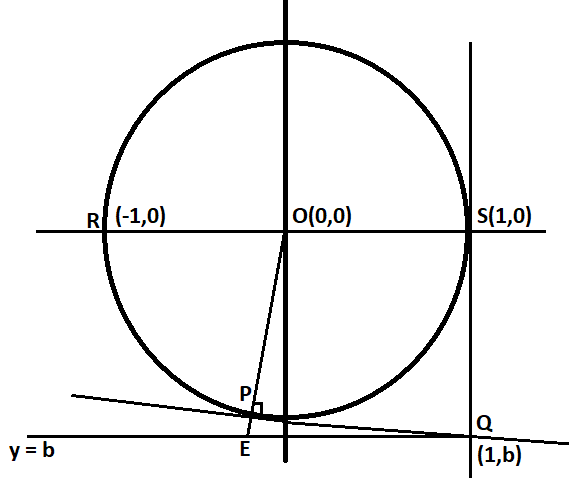



Let Rs Be The Diameter Of The Circle X2 Y2 1 Where Class 12 Maths Cbse




Circles And Tangent Lines




Find A Parameterization For The Circle X 2 2 Y 2 1 Starting At The Point 1 0 And Moving Clockwise Twice Around The Circle Using The Central Angle 0 In The Figure Below




In The Xy Plane Point X Y Lies On The Circle With Equation X 2 Y 2 1 And On The Line With The Equation Y 2x What Is The Value Of Xy Pwn Test Prep




Plotting All Of A Trigonometric Function X 2 Y 2 1 With Matplotlib And Python Stack Overflow
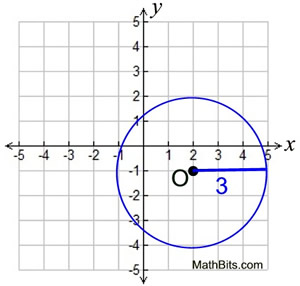



Circle Equations Mathbitsnotebook Geo Ccss Math




A Circle Through The Common Points Of The Circles X 2 Y 2 2x 4y 1 0 And X 2 Y 2 2x 6y 1 0 Has The Centre On The Line 4y 7x 19 0 Find The Centre And Radius Of The Circle Homeworklib




If A Diameter Of The Circle X 2 Y 2 2x 6y 6 0 Is A Chord Of Another Circle C Having Centre 2 1 Then The Radius Of The Circle C Is
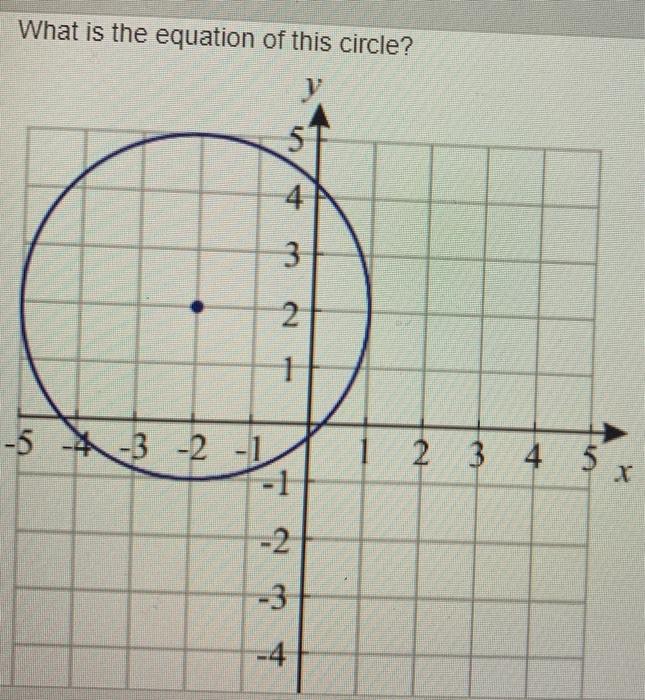



Solved What Is The Equation Of This Circle 4 3 2 1 5 Chegg Com




Find The Area Of The Region Inside The Circle X 1 2 Y 2 1 And Outside The Circle X 2 Y 2 1 Study Com




Pin On Equations For Shapes




Prove That The Unit Circle X 2 Y 2 1 Is A Closed Set Newbedev



1
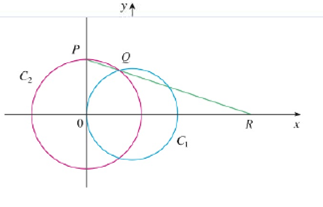



The Figure Shows A Fixed Circle C 1 With Equation X 1 2 Y 2 1 And A Shrinking Circle C With Radius R And



Www Npsk12 Com Cms Lib Va Centricity Domain 37 Geometry Pdf




Consider A Circle X 2 Y 2 1
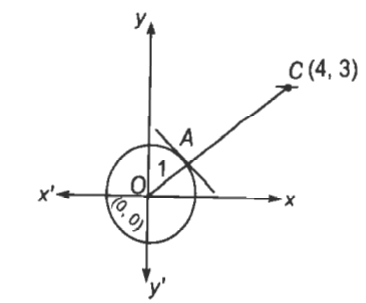



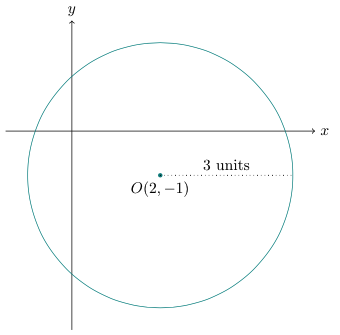
Equation Of The Circle Centered At 4 3 Touching The Circl




How To Imagine X 2 Y 2 1 0 In C 2 X Y Both Complex Mathematics Stack Exchange




If X Y Lies On Circle X 2 Y 2 1 Then Maximum Value Of X Y 2 Youtube




The Circle X 2 Y 2 2x 2y 1 0 Is Rolled Along The Positive Direction Of X Axis And Makes One Youtube




Find The Area Of The Smaller Part Of The Circle X2 Y2 Cut Off By The Line X A Sqrt2 Mathematics Shaalaa Com



How To Draw X 2 Y 2 1 Quora




Circle Equation More Examples




The Tangent To The Circle X 2 Y 2 5 At The Point 1 2 Also Touches The Circle X 2 Y 2 8x 6y 0 At




Describe All Integral Solutions Of The Equation X 2 Y 2 2z 2 Such That X Y Z 0 Gcd X Y Z 1 And X Y Mathematics Stack Exchange



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic




Do Now Graph The Equation X 2 Y 2 1 Draw And Label The Special Right Triangles What Happens When The Hypotenuse Of Each Triangle Equals 1 Ppt Download


